什么是风险?
人们常说”高风险, 高回酬”. 可是如果承受高的风险, 真的可以给你高回酬的话, 那这些投资还算是高风险吗?
我发现美国橡树资本的Howard Marks对风险的看法很有意思.
根据Howard Marks的说法, 当你承受高风险时, 你的回酬会承受更高的波动. 一图胜千言.

不同的资产等级有它们的风险等级.
股票型资产通常给人比较高风险的感觉, 股票型资产的回酬比较多不确定性, 有时候非常高, 有时候非常低甚至是负数, 主要的回酬范围在-20至50% (我们讨论的是大市而不是个股).
因为很多变数可以影响股票的回酬, 市场情况, 公司盈利, 新的竞争者等.
反之债券型资产就比较低风险, 债券型资产回酬通常是非常低不确定性, 所以有时候债券也被称为fixed income asset.
债券的主要风险在于公司/国家的倒闭, 无法偿还债券的利息或本金.
投资界大佬之一 John Bogle 的策略
John Bogle 是 The Vanguard Group 的创办人, The Vanguard Group是美国数一数二的资产管理公司.
他投资的方法是把股票与债券分配至50/50的比例, 就是持有相同价值的股票与债券资产.
打个例子
| 股票 | 债券 |
|---|---|
| 5500 | 5100 |
此时你必须把RM400从股票资产转移至债券资产, 所以才符合50/50的原则.
这个方法的目的是要重新调整资产组合, 一个价钱高的资产有可能是被高估了, 所以需要套利并把资金移入另一个资产.
反之如果股票资产的价钱低了, 你就需要把资金从债券移至股票, 趁股票资产被低估的时候买进.
分析方法
我从morningstar的网站爬取的本地著名基金公司 “P公司” 的数据.
股票型基金我用的数据是 Global Equity Fund, East-Asia Equity Fund, Malaysia Index Fund. 选这3个基金的原因是因为它们可以很好的跟踪全球各国股市的表现.
债券型基金我用的数据是 Enhanced Bond Fund.
数据的时间是从2006至2020, 以模拟长期投资的效果.
我用Python来计算各个rebalance, 资产增值的计算, 厉害用Excel的大神也可以用Excel, 只是我对Python比较熟悉所以用的是Python.
初始化
我们需要pandas来做数据分析, 而seaborn及matplotlib用于数据可视化.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
#read portfolio data
Return = pd.DataFrame()
p = pd.read_csv('Portfolio.csv', parse_dates=['Date'])
Return['Date'] = p['Date']
Return['Date'] = pd.DatetimeIndex(Return['Date']).year.astype(float)
print(p.head)数据分析
一些基本的逻辑算法
def CalculateReturn(Equity,Bond,Investment):
# Equity
PGSF = 0.15
PIX = 0.15
PFES = 0.7
# Bond
PBOND = 1.0
portfolio = pd.read_csv('Portfolio.csv', parse_dates=['Date'])
EquityInvestment = Equity*Investment
BondInvestment = Bond*Investment
portfolio['PGSF Value'] = ""
portfolio['PIX Value'] = ""
portfolio['PFES Value'] = ""
portfolio['PBOND Value'] = ""
portfolio['Rebalanced E'] = ""
portfolio['Rebalanced B'] = ""
#first year value
portfolio['PGSF Value'][0] = EquityInvestment * PGSF * portfolio['PGSF'][0]
portfolio['PIX Value'][0] = EquityInvestment * PIX * portfolio['PIX'][0]
portfolio['PFES Value'][0] = EquityInvestment * PFES * portfolio['PFES'][0]
portfolio['PBOND Value'][0] = BondInvestment * PBOND * portfolio['PBOND'][0]
portfolio['Rebalanced E'][0] = portfolio['PGSF Value'][0] + portfolio['PIX Value'][0] + portfolio['PFES Value'][0]
portfolio['Rebalanced B'][0] = portfolio['PBOND Value'][0]
for i in range(1,15):
portfolio['PGSF Value'][i] = portfolio['Rebalanced E'][i-1] * PGSF * portfolio['PGSF'][i]
portfolio['PIX Value'][i] = portfolio['Rebalanced E'][i-1] * PIX * portfolio['PIX'][i]
portfolio['PFES Value'][i] = portfolio['Rebalanced E'][i-1] * PFES * portfolio['PFES'][i]
portfolio['PBOND Value'][i] = portfolio['Rebalanced B'][i-1] * PBOND * portfolio['PBOND'][i]
totalVal = portfolio['PGSF Value'][i] + portfolio['PIX Value'][i] + portfolio['PFES Value'][i] + portfolio['PBOND Value'][i]
portfolio['Rebalanced E'][i] = totalVal * Equity
portfolio['Rebalanced B'][i] = totalVal * Bond
portfolio['Total'] = portfolio['Rebalanced B'] + portfolio['Rebalanced E']
return portfolio['Total']
Return['Equity'] = CalculateReturn(1,0,20000).astype(float)
Return['Bond'] = CalculateReturn(0,1,20000).astype(float)
Return['50/50 Equity/Bond'] = CalculateReturn(0.5,0.5,20000).astype(float)
print(Return)
输出
完成数据分析后的数据可视化
sns.set_style("darkgrid")
p = sns.color_palette("hls", 8)
ax = sns.lineplot(data=Return,y='Equity',x='Date',label="Full Equity", color='skyblue', marker='^',markeredgecolor="black",linewidth=5)
ax = sns.lineplot(data=Return,y='Bond',x='Date',label="Full Bond",color='lightcoral',marker="x",markeredgecolor="black",linewidth=5)
ax = sns.lineplot(data=Return,y='50/50 Equity/Bond',x='Date',color='palegreen',label="50/50 Equity/Bond",marker="o",markeredgecolor="black",linewidth=5)
ax.set(xlabel="Date",ylabel="RM10k Invested")
plt.legend()
plt.show()分析数据
| 满仓股票 | 满仓债券 | 50/50 股票/债券 | |
|---|---|---|---|
| 回酬率 | 270% | 105% | 244% |
| 2020年资产价值 | 27142 | 18664 | 24482 |
| 最低点 | 9971 | 10532 | 11191 |

如果你每年加码呢?
我也计算了如果每年加码RM1000的结果, 就如预算的, 资产增值的速度会增快.
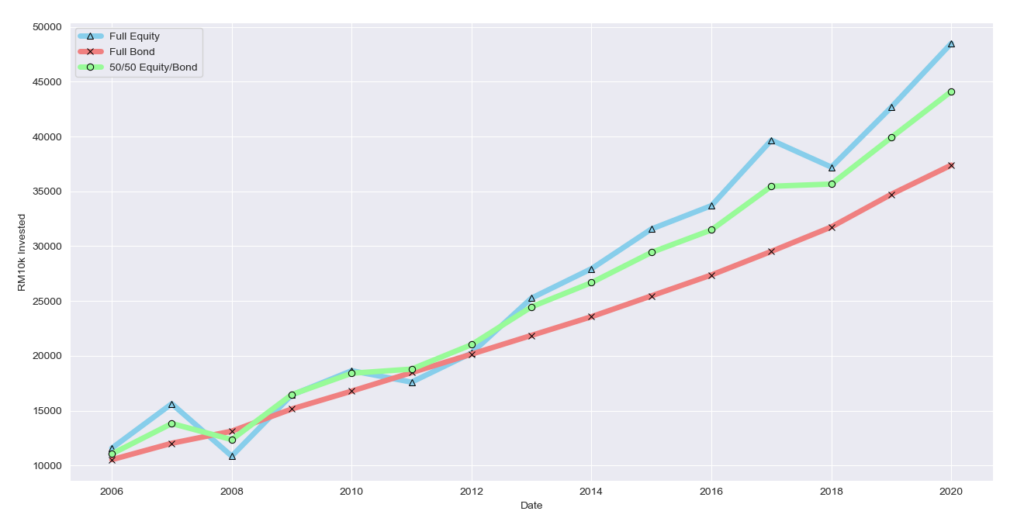
总结
- 不错的 风险/回酬 比例. 50/50组合可以在降低风险的情况下保持回酬.
- 分散风险不一定会牺牲高回酬. 50/50组合在更小的波动下只比股票型资产少赚了10% (大概RM2600)
- Rebalance不能太常进行, 必须考虑到手续费.
